Showing posts with label programming. Show all posts
Showing posts with label programming. Show all posts
Wednesday, 7 August 2013
Compile 32 Bit Binaries On 64 Bit Machine
Well I had this special need if you recall my previous blog post since my friend had 64 bit machine. Sometimes, there might be this necessity to compile 32 bit binaries on your 64 bit machine. This post describes how to do so.
First make sure the necessary x86 libraries are installed. We require 32-bit shared libraries for AMD64 to compile binaries in 32 bit format. The command below installs the i386 version of libc6-dev:
Now you can compile your code in 32 bit binary format using the -m32 flag where 32 represents the x86 processor (-m64 would mean x64 processor).
I hope this helps :)
Read more...
First make sure the necessary x86 libraries are installed. We require 32-bit shared libraries for AMD64 to compile binaries in 32 bit format. The command below installs the i386 version of libc6-dev:
$ sudo apt-get install libc6-dev-i386
Now you can compile your code in 32 bit binary format using the -m32 flag where 32 represents the x86 processor (-m64 would mean x64 processor).
$ gcc -m32 -o test test.c
I hope this helps :)
Read more...
Compile 32 Bit Binaries On 64 Bit Machine
2013-08-07T16:13:00+05:45
Cool Samar
c|C/C++|linux|programming|ubuntu|
Comments
Labels:
c,
C/C++,
linux,
programming,
ubuntu
Bookmark this post:blogger tutorials
Social Bookmarking Blogger Widget |
Pointers Without Pointer Variables
Since a pointer variable is nothing but a variable holding 4 bytes memory address (at least on 32-bit addressing), I had a thought that non-pointer variables which can hold 4-bytes of data can be used in place of pointer variables. This post shows how this can be achieved.
The code example below uses an unsigned integer variable in order to store memory addresses to point the integer array.
The same concept can be used to use non-pointer variable for pointing other datatypes. After all, its about correct type-casting and since 4 bytes datatype can hold memory addresses, pointer is not always necessary. It must be noted that the increment would be different for different datatypes. Since integer requires 4 bytes, ptr is incremented in this example. If we had character array, then ptr would have to be increased by 1 since char type requires 1 byte.
However, pointers are there to make our life easy. It was just for fun :)
Read more...
The code example below uses an unsigned integer variable in order to store memory addresses to point the integer array.
#includeint main(int argc, char **argv) { int num[] = {1, 2, 3, 4, 5}; unsigned int ptr; int i; ptr = (unsigned int) num; for (i = 0; i < 5; i++) { printf("%p - %d\n\n", (void *) ptr, *(int *)(ptr)); ptr = ptr + 4; } return 0; }
The same concept can be used to use non-pointer variable for pointing other datatypes. After all, its about correct type-casting and since 4 bytes datatype can hold memory addresses, pointer is not always necessary. It must be noted that the increment would be different for different datatypes. Since integer requires 4 bytes, ptr is incremented in this example. If we had character array, then ptr would have to be increased by 1 since char type requires 1 byte.
However, pointers are there to make our life easy. It was just for fun :)
Read more...
Pointers Without Pointer Variables
2013-08-07T13:42:00+05:45
Cool Samar
c|C/C++|programming|
Comments
Labels:
c,
C/C++,
programming
Bookmark this post:blogger tutorials
Social Bookmarking Blogger Widget |
Wednesday, 12 June 2013
Simple Pie Chart Implementation In Turbo C
This is a very simple implementation of pie chart in Turbo C. The source code is quite easy to read through so must not be the big problem understanding the code.
This implementation makes use of pieslice() function which draws and fills the pie slice with centre x, y and radius r. The function also requires the start angle and end angle.
Below is the screenshot for sample run:
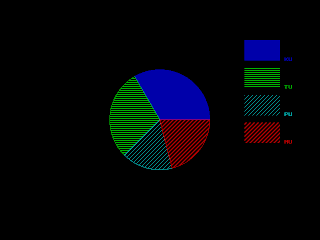
Read more...
This implementation makes use of pieslice() function which draws and fills the pie slice with centre x, y and radius r. The function also requires the start angle and end angle.
#include <stdio.h>
#include <conio.h>
#include <graphics.h>
#include <math.h>
#define MAX 20
#define X_CENTRE getmaxx()/2
#define Y_CENTRE getmaxy()/2
#define RADIUS 100
struct pie_data
{
char desc[100];
int freq;
int color;
int style;
float angle;
};
int main()
{
struct pie_data data[MAX];
int gd = DETECT, gm;
int i, j, k, n, total_freq = 0, start_angle = 0, end_angle = 0, xmax, ystart = 80, yend;
printf("Enter the number of items: ");
scanf("%d", &n);
for (i = 0, j = 1, k = 1; i < n; i++)
{
printf("Enter the item title: ");
scanf("%s", data[i].desc);
printf("Enter the item frequency: ");
scanf("%d", &data[i].freq);
total_freq += data[i].freq;
data[i].color = j;
data[i].style = k;
if (j++ >= 13) j = 1;
if (k++ >= 11) k = 1;
}
for (i = 0; i < n; i++)
{
float angle;
data[i].angle = 360 * (data[i].freq /(float) total_freq);
}
initgraph(&gd, &gm, "C:\\TurboC3\\BGI");
xmax = getmaxx() - 150;
setaspectratio(10000, 10000);
for (i = 0; i < n; i++)
{
end_angle = start_angle + data[i].angle;
setcolor(data[i].color);
setfillstyle(data[i].style, data[i].color);
pieslice(X_CENTRE, Y_CENTRE, (int)start_angle, (int)end_angle, RADIUS);
start_angle = end_angle;
yend = ystart + 40;
bar(xmax, ystart, xmax + 70, yend);
ystart = yend + 15;
outtextxy(xmax + 80, ystart - 20, data[i].desc);
}
getch();
closegraph();
return 0;
}
Below is the screenshot for sample run:
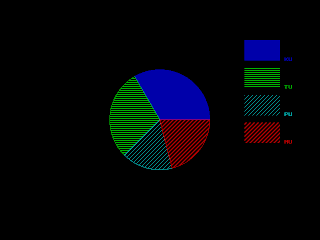
Read more...
Simple Pie Chart Implementation In Turbo C
2013-06-12T10:09:00+05:45
Cool Samar
c|C/C++|computer graphics|programming|
Comments
Labels:
c,
C/C++,
computer graphics,
programming
Bookmark this post:blogger tutorials
Social Bookmarking Blogger Widget |
Sunday, 31 March 2013
Simple Line Drawing In Turbo C Graphics
Well this post consists of the source code for very very simple line drawing using the in-built functions.
I hope it proves useful for learning purpose.
Read more...
#include <stdio.h>
#include <conio.h>
#include <graphics.h>
int main()
{
int gd = DETECT, gm;
initgraph(&gd, &gm, "C:\\TurboC3\\BGI");
line(100, 100, 350, 100);
line(100, 100, 70, 140);
line(70, 140, 130, 140);
line(350, 100, 380, 140);
rectangle(70, 140, 130, 200);
rectangle(130, 140, 380, 200);
getch();
closegraph();
return 0;
}
I hope it proves useful for learning purpose.
Read more...
Simple Line Drawing In Turbo C Graphics
2013-03-31T23:00:00+05:45
Cool Samar
c|C/C++|programming|
Comments
Labels:
c,
C/C++,
programming
Bookmark this post:blogger tutorials
Social Bookmarking Blogger Widget |
Implementation Of BLA Line Drawing Algorithm
Here is the source code that makes use of the traditional DOS mode graphics to implement the Bresenham line drawing algorithm for the lines with slope |m| < 1.
1) Input two points (x1, y1) & (x2, y2).
2) Determine the differences dx = x2 - x1 and dy = y2 - y1.
3) Calculate the initial decision parameter P0 = 2dy - dx.
4) For each xk along the line starting at k = 0,
if Pk < 0,
a) put a pixel at (xk + 1, yk)
b) Pk+1 = Pk + 2dy
else
a) put a pixel at (xk + 1, yk + 1)
b) Pk+1 = Pk + 2dy - 2dx.
5) Repeat step 4 for dx time.
6) End
Make sure to provide an appropriate path for graphics library.
Read more...
Bresenham Line Drawing Algorithm for |m| < 1
Algorithm
1) Input two points (x1, y1) & (x2, y2).
2) Determine the differences dx = x2 - x1 and dy = y2 - y1.
3) Calculate the initial decision parameter P0 = 2dy - dx.
4) For each xk along the line starting at k = 0,
if Pk < 0,
a) put a pixel at (xk + 1, yk)
b) Pk+1 = Pk + 2dy
else
a) put a pixel at (xk + 1, yk + 1)
b) Pk+1 = Pk + 2dy - 2dx.
5) Repeat step 4 for dx time.
6) End
Source Code
#include <stdio.h>
#include <conio.h>
#include <graphics.h>
#include <math.h>
int main()
{
int gd = DETECT, gm;
int x1, y1, x2, y2, dx, dy;
int x, y, i, p0, pk;
printf("Enter x1, y1: ");
scanf("%d %d", &x1, &y1);
printf("Enter x2, y2: ");
scanf("%d %d", &x2, &y2);
dx = x2 - x1;
dy = y2 - y1;
x = x1;
y = y1;
p0 = ( 2 * dy - dx);
initgraph(&gd, &gm, "C:\\TurboC3\\BGI");
pk = p0;
for (i = 0; i < abs(dx); i++)
{
if (pk < 0)
{
putpixel(x, y, WHITE);
pk += (2 * dy);
}
else
{
putpixel(x, y, WHITE);
pk += (2 * dy - 2 * dx);
}
(x1 < x2)?x++:x--;
(y1 < y2)?y++:y--;
delay(50);
}
getch();
closegraph();
return 0;
}
Make sure to provide an appropriate path for graphics library.
Read more...
Implementation Of BLA Line Drawing Algorithm
2013-03-31T22:05:00+05:45
Cool Samar
c|C/C++|computer graphics|programming|
Comments
Labels:
c,
C/C++,
computer graphics,
programming
Bookmark this post:blogger tutorials
Social Bookmarking Blogger Widget |
Tuesday, 26 March 2013
Implementation of DDA Line Drawing Algorithm
Here is a source code in traditional Turbo C that makes use of old DOS mode graphics to implement the digital differential analyzer.
2) Determine the differences dx = x2 - x1 and dy = y2 - y1.
3) Choose step size as the bigger value between the absolute values of dx and dy.
4) Determine x-increment = dx/step_size and y-increment = dy/step_size.
5) Start from (x0, y0) = (x1, y1).
6) For i -> 0 to stepsize:
a) draw pixel at (xi, yi)
b) set xk = xk + x-increment
b) set yk = yk + y-increment
Make sure to provide an appropriate path for graphics library.
Read more...
Digital Differential Analyzer
Algorithm
1) Input two points (x1, y1) & (x2, y2).2) Determine the differences dx = x2 - x1 and dy = y2 - y1.
3) Choose step size as the bigger value between the absolute values of dx and dy.
4) Determine x-increment = dx/step_size and y-increment = dy/step_size.
5) Start from (x0, y0) = (x1, y1).
6) For i -> 0 to stepsize:
a) draw pixel at (xi, yi)
b) set xk = xk + x-increment
b) set yk = yk + y-increment
Source Code
#include <stdio.h>
#include <conio.h>
#include <graphics.h>
#include <math.h>
int main()
{
int gd = DETECT, gm;
int x1, y1, x2, y2, dx, dy, stepsize;
float xinc, yinc, x, y;
int i;
printf("Enter x1, y1: ");
scanf("%d %d", &x1, &y1);
printf("Enter x2, y2: ");
scanf("%d %d", &x2, &y2);
dx = x2 - x1;
dy = y2 - y1;
stepsize = (abs(dx) > abs(dy))?abs(dx):abs(dy);
xinc = dx/(float)stepsize;
yinc = dy/(float)stepsize;
x = x1;
y = y1;
initgraph(&gd, &gm, "C:\\TC\\BGI");
putpixel(x, y, WHITE);
delay(10);
for (i = 0; i < stepsize; i++)
{
x += xinc;
y += yinc;
putpixel(x, y, WHITE);
delay(50);
}
getch();
closegraph();
return 0;
}
Make sure to provide an appropriate path for graphics library.
Read more...
Implementation of DDA Line Drawing Algorithm
2013-03-26T01:08:00+05:45
Cool Samar
c|C/C++|computer graphics|programming|
Comments
Labels:
c,
C/C++,
computer graphics,
programming
Bookmark this post:blogger tutorials
Social Bookmarking Blogger Widget |
Tuesday, 22 January 2013
Simple Sorting Algorithm Using DMA
This post provides the source code for simple and naive integer sorting algorithm by exploiting the dynamic memory allocation feature of C programming.
Read more...
#include <stdio.h>
#include <stdlib.h>
int main()
{
int *arr, i, j, n;
printf("Enter the number of items: ");
scanf("%d", &n);
arr = malloc(n * sizeof(int));
for (i = 0; i < n; i++)
{
printf("Enter the %dth item: ", i + 1);
scanf("%d", &arr[i]);
}
for (i = 0; i < n - 1; i++)
{
for (j = 0; j < n - 1; j++)
{
int temp;
if (arr[j] > arr[j + 1])
{
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
printf("The sorted array is:\n");
for (i = 0; i < n; i++)
{
printf("%d\n", arr[i]);
}
return 0;
}
samar@samar-Techgaun:~$ gcc -Wall -o sort sort.c samar@samar-Techgaun:~$ ./sort Enter the number of items: 5 Enter the 1th item: 2 Enter the 2th item: 4 Enter the 3th item: 1 Enter the 4th item: 92 Enter the 5th item: 45 The sorted array is: 1 2 4 45 92
Read more...
Simple Sorting Algorithm Using DMA
2013-01-22T16:54:00+05:45
Cool Samar
beginner|c|C/C++|programming|
Comments
Labels:
beginner,
c,
C/C++,
programming
Bookmark this post:blogger tutorials
Social Bookmarking Blogger Widget |
Matrix Multiplication Using DMA [C Source Code]
This post provides a source code for matrix multiplication by dynamically allocating memory for matrices to be multiplied and multiplication of those matrices.
Read more...
#include <stdio.h>
#include <stdlib.h>
int main()
{
int **A, **B, **C, m, n, p, q, i, j, k;
printf("Enter the size of matrix A: ");
scanf("%d %d", &m, &n);
printf("Enter the size of matrix B: ");
scanf("%d %d", &p, &q);
if (n == p)
{
A = malloc(m * sizeof(int));
B = malloc(p * sizeof(int));
C = malloc(m * sizeof(int));
for (i = 0; i < m; i++)
{
A[i] = malloc(n * sizeof(int));
C[i] = malloc(q * sizeof(int));
}
for (i = 0; i < p; i++)
{
B[i] = malloc(q * sizeof(int));
}
printf("Enter the matrix A:\n\n");
for (i = 0; i < m; i++)
{
for (j = 0; j < n; j++)
{
scanf("%d", &A[i][j]);
}
}
printf("Enter the matrix B:\n\n");
for (i = 0; i < p; i++)
{
for (j = 0; j < q; j++)
{
scanf("%d", &B[i][j]);
}
}
for (i = 0; i < m; i++)
{
for (j = 0; j < q; j++)
{
C[i][j] = 0;
for (k = 0; k < n; k++)
{
C[i][j] = C[i][j] + (A[i][k] * B[k][j]);
}
}
}
printf("Multiplication of given matrices is: \n\n");
for (i = 0; i < m; i++)
{
for (j = 0; j < q; j++)
{
printf("%d ", C[i][j]);
}
printf("\n");
}
for (i = 0; i < m; i++)
{
free(A[i]);
free(C[i]);
}
for (i = 0; i < p; i++)
{
free(B[i]);
}
free(A);
free(B);
free(C);
}
else
{
printf("Matrix multiplication is not possible for given size\n\n");
}
return 0;
}
samar@samar-Techgaun:~$ gcc -Wall -o matrix_mul matrix_mul.c samar@samar-Techgaun:~$ ./matrix_mul Enter the size of matrix A: 3 2 Enter the size of matrix B: 2 3 Enter the matrix A: 1 2 3 4 5 6 Enter the matrix B: 1 2 3 4 5 6 Multiplication of given matrices is: 9 12 15 19 26 33 29 40 51
Read more...
Matrix Multiplication Using DMA [C Source Code]
2013-01-22T16:47:00+05:45
Cool Samar
beginner|c|C/C++|programming|
Comments
Labels:
beginner,
c,
C/C++,
programming
Bookmark this post:blogger tutorials
Social Bookmarking Blogger Widget |
Subscribe to:
Comments (Atom)